remembering Thomas Harriot, 400 years on
- Written by Robyn Arianrhod, Affiliate, School of Mathematics, Monash University
Four hundred years ago, on July 2 1621, a remarkable Englishman named Thomas Harriot died in London. He left behind some 8,000 pages of scientific research, but it is only in recent decades that scholars have uncovered their treasures.
And what they show is that Harriot independently made many significant discoveries now attributed to other, more famous scientists. Some scholars have called him “the English Galileo” and “the greatest British mathematical scientist before Newton”.
Yet Harriot died without publishing a single word of this extraordinary output. His tale reminds us that, while we may sometimes think science progresses through a series of famous pioneers who single-handedly overturn entrenched beliefs, the story is rarely so simple.
What did Harriot discover?
For instance, we learn in school that Galileo Galilei initiated telescopic astronomy and discovered the law of falling motion. But Harriot independently did both of these things.
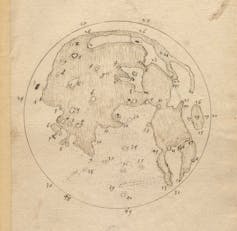 Thomas Harriot’s 1609 map of the Moon, drawn by observing through a telescope.
Wikimedia[1]
Thomas Harriot’s 1609 map of the Moon, drawn by observing through a telescope.
Wikimedia[1]
He also deduced fledgling general laws governing the motion of everyday objects, again independently of Galileo, and before René Descartes. (Half a century later, Isaac Newton developed the definitive laws of motion.)
Harriot studied light, too, discovering the secret of colour and the nature of the rainbow before Newton, and finding the law of refraction (which we know today as Snell’s law) before the Dutch astronomer Willebrord Snell.
He also made a mathematical study of population growth before Thomas Malthus, developed a completely symbolic[2] form of sophisticated algebra[3] before Descartes, discovered binary arithmetic before Gottfried Leibniz, and took steps on the road to calculus with his work on infinite series.
The law of falling bodies
It wasn’t until 2008 that Harriot’s work on gravity was fully reconstructed[4], by the German scholar Matthias Schemmel.
As Schemmel pointed out, Harriot and his contemporary Galileo were heirs to essentially the same body of knowledge. It’s perhaps not so surprising, then, that they made some of the same breakthroughs. There are plenty of examples of independent co-discoveries in history, most famously that of calculus by Newton and Leibniz.
The law of falling motion says that without air resistance all objects, no matter their size or mass, fall from the same height at the same rate.
Legend has it Galileo dropped balls from the Leaning Tower of Pisa to study how they fell. Nobody knows if this is true, but Harriot had the same idea: he recorded the time, in pulse beats, that it took for different objects falling from as high as 55½ feet (about 17 metres) to reach the ground.
Read more: Copernicus' revolution and Galileo's vision: our changing view of the universe in pictures[5]
Both Harriot and Galileo devised more accurate experiments, however, from which they derived a mathematical understanding of how things fall.
This combination of experiment and mathematics is now the accepted way to derive a law of nature. Quantifying observations means others can test the results, and use them to make useful predictions.
Harriot and Galileo were not the first to understand the role of observation and mathematics in this context, of course. But they were among the most successful of the pre-Newtonian pioneers.
Galileo didn’t publish his work on gravity until after Harriot had died, and there’s no evidence that the two men ever met or corresponded.
The law of refraction and the shape of the rainbow
The German astronomer Johannes Kepler, however, did correspond briefly with Harriot. Kepler had been working on the nature of light and vision when word reached him that Harriot had unravelled two mysteries: the law of refraction, and why the rainbow has its magical colours and its unique shape.
The law of refraction describes how light bends when it passes from one medium into another, which explains how an image can be focused by a glass lens or why your leg looks wobbly when you dip it in a swimming pool.
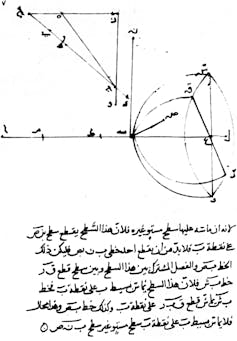 A diagram from Ibn Sahl’s 10th-century treatise on optics showing the path of light refracted by a lens.
Wikimedia[6]
A diagram from Ibn Sahl’s 10th-century treatise on optics showing the path of light refracted by a lens.
Wikimedia[6]
Harriot derived this law 20 years before Snell, but there’s a popular belief that the 10th-century Baghdad-based scholar Abū Saʿd al-ʿAlāʾ ibn Sahl beat even Harriot. This is not quite right: Ibn Sahl is a notable pioneer whose geometrical diagram of light focussed by a lens gives, in hindsight, the correct refractive path. But there’s no evidence he deduced his result from experiment, or that he understood the general properties of refraction.
Judging from his surviving papers even Snell failed to generalise his result, which he, like Ibn Sahl, never wrote as the neat trigonometric equation we use today. Harriot, by contrast, did: his derivation of the general law of refraction is another example of his rigorous blend of experiment and mathematics.
Read more: Curious Kids: Why are rainbows round?[7]
Harriot’s other adventures
If only Harriot had published! In the early stage of his career, though, he was bound by commercial secrecy, for his first patron was the controversial statesman and entrepreneur Sir Walter Raleigh. Harriot was also busy dodging heretic hunters and sailing the high seas as Raleigh’s navigational advisor.
 Thomas Harriot published only one work in his lifetime: a report on his stay in North America in the 1580s.
Wikimedia[8]
Thomas Harriot published only one work in his lifetime: a report on his stay in North America in the 1580s.
Wikimedia[8]
Raleigh had delusions of empire and glory, and wanted to establish a trading colony in today’s USA before the Spanish beat him to it. The one work Harriot did publish in his lifetime was “a brief and true report” on the economic potential of Raleigh’s chosen American site.
Harriot’s contribution to colonialism has justly attracted its share of criticism. Nonetheless, his report is still widely praised for its sympathetic depiction of the way of life of the North Carolina Algonquian people, as it was when Europeans first set foot on their land. Harriot learned the local language, and enjoyed much about the year he spent living with the Algonquians.
What he loved doing most, though, was mathematics and physics. He was neither flamboyant nor ambitious, and when he was wrongfully imprisoned through an unlucky connection with the Gunpowder Plot (a failed attempt to assassinate King James I), he told his jailers he just wanted
to live a private life for the love of learning that I might study freely.
Conclusion
In the late 1590s Harriot had found a second patron, Henry Percy, the ninth earl of Northumberland. It was then that he was able to study the mysteries of nature and the marvels of mathematics for their own sakes, rather than the “applied” work he had done for Raleigh.
Having two generous patrons meant Harriot did not need to publicise his discoveries to attract funding, the way Galileo did. Nor did he care about fame, despite being urged by friends to claim his priority. His manuscripts do contain several almost finished treatises, but it seems he was so busy doing science that he never managed to put his results together for the printer.
After his death, well-meaning scholars carved up his manuscripts in an attempt to study and publish them. In the process, however, all the papers disappeared, seemingly lost forever. Then, 150 years later, the Hungarian astronomer Franz Xaver Zach discovered them, locked safely away in Northumberland’s castle.
Most of the papers were then given to the British Museum. They are now in the British Library, where I had the privilege of studying them. (They’re also available online[9].)
As for Harriot, no-one knows much about him as a person – not even his birthday. Nevertheless, he has fascinated scholars for the past half century (as I discovered some years ago when I set out to bring his story to a wider, non-specialist[10] readership).
That’s because despite the lack of biographical data, those precious manuscripts show that what mattered most to Harriot himself was mathematics and science. Four hundred years on, his mix of genius and dedication is something to honour.
References
- ^ Wikimedia (en.wikipedia.org)
- ^ completely symbolic (www.ems-ph.org)
- ^ algebra (www.springer.com)
- ^ fully reconstructed (www.springer.com)
- ^ Copernicus' revolution and Galileo's vision: our changing view of the universe in pictures (theconversation.com)
- ^ Wikimedia (en.wikipedia.org)
- ^ Curious Kids: Why are rainbows round? (theconversation.com)
- ^ Wikimedia (en.wikipedia.org)
- ^ online (echo.mpiwg-berlin.mpg.de)
- ^ wider, non-specialist (global.oup.com)

















